What is the point of learning fractions, particularly how to add, subtract, multiply and divide them, when we have calculators that can everything for us?

One answer is that when you use a calculator you should understand what the calculator is doing. Or some time you may need to do a calculation with fractions and not have a calculator around (like on parts of standardized tests).

I think a much better reason for knowing fractions is that the techniques you learn for fractions are exactly the same ones you will need for parts of algebra. If you don't understand and master the ideas for fractions, then you will find learning algebra difficult. Let's see some examples of how the techniques of fractions transfer to algebra.

Algebra involves quantities called variables (that can represent values perhaps not yet known). One kind of formula in algebra that has one or more variables is called a rational expression. Adding and subtracting rational expressions is just like adding and subtraction fractions - you need to use a common denominator.

Example 1: Perform the subtraction of rational expressions:

As with fractions, the first step is to find a common denominator. Since we don't know what the denominators (x+3) and (x-2) equal (as numbers - it depends on what x represents), we take the product (x+3)(x-2) as the common denominator. We then have to represent each of the two rational expressions using the common denominator. Just multiply the numerator of each expression by the same factor introduced into its denominator:

Since the denominators of the two expressions are now the same, the calculation can be completed by combining the fractions, which means subtracting the numerators:

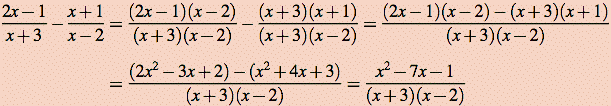
That's it. Just like subtracting fractions!

Try one yourself. Click on the colored text when you think you have an answer for each step of the solution.

Example 2: Perform the addition of rational expressions:

Find the common denominator of the two rational expressions. Click to see the answer. Click to remove answer.

Common denominator =

Express the first rational expression using the common denominator. Click to see the answer. Click to remove answer.

Express the second rational expression using the common denominator. Click to see the answer. Click to remove answer.

Add the two expressions using the common denominator forms. Click to see the answer. Click to remove answer.

Once again, the steps are just the same as those used to add two fractions. Multiplying and dividing rational expressions mimics multiplying and dividing fractions in the same way.

Let's summarize. The two examples we saw would be difficult to understand without properly understanding how to add and subtract fractions. There are many ideas you learn in math that may not seem immediately important, but are very important for understanding new concepts in later math classes. Learning how to compute with fractions is one of these ideas.